Lo sciatore e la relatività ristretta

Eccoci arrivati alla terza puntata (leggi la prima e la seconda) di questa miniserie sulla relatività ristretta. Avendo acquisito tutti gli strumenti necesssari, oggi discuteremo finalmente del paradosso dello sciatore.
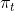
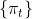
Notiamo preliminarmente che un punto è rappresentato in un diagramma spaziotemporale da una retta, e tutti i punti di un corpo rigido sono rappresentati da rette parallele. L'insieme dei punti sincronizzati a un determinato tempo t di questo sistema sono rappresentati da piani perpendicolari all'asse temporale ct. Ogni sistema di riferimento avrà una famiglia di piani diversa e questo rappresenta geometricamente la relatività della simultaneità.


Fatta questa premessa, illustriamo la situazione dello sciatore e della buca in un diagramma spaziotemporale (questa figura è ripresa identica dall'articolo di Elio Fabri citato nelle fonti):

Supponiamo per generalità che sia la buca che gli sci siano in moto.

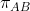
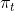
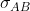
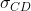
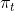
Gli sci individuano una striscia definita dalle linee orarie degli estremi A e B e definiscono quindi un piano . In maniera analoga, la buca è definita dai suoi estremi C e D, che definiscono un piano . Nel riferimento in quiete K, un dato istante t definisce un piano . Le intersezioni delle due strisce e con il piano rappresentano le posizioni all'istante t della buca e degli sci e dalle condizioni del problema è evidente che queste sono parallele. 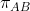Ne consegue che anche l'intersezione di e è una retta (indicata con R) ed è parallela al piano . 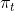Questa intersezione rappresenta l'istante in cui gli sci e la buca si incrociano e quindi sono sulla stessa retta e dimostra che il sistema K è quello più semplice per descrivere il paradosso. A ben vedere K non è l'unico sistema che gode di questa particolarità, ma vale per ogni sistema rappresentato da piani paralleli a R e in particolare quello in cui la buca è ferma.

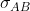
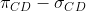
Perché lo sci cada nella buca basta evidentemente che non intersechi , ovvero che . I quattro punti M, N, P e Q sono eventi nello spaziotempo di Minkowski e pertanto le distanze sono invarianti, deve quindi risultare . Questa condizione non dipende dal sistema di riferimento e pertanto non esiste alcun paradosso!. In particolare, nel riferimento K queste distanze coincidono con le distanze euclidee e pertanto questo sistema risulta particolarmente comodo per "risolvere" il paradosso. Quello che conta quindi è che nel sistema K gli sci siano più corti della buca.

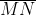
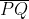
Nel sistema K' degli sci, il problema risulta invece particolarmente complesso da trattare. I piani di questo sistema non sono paralleli a R e di conseguenza le lunghezze calcolate in questo sistema non sono utilizzabili per risolvere il problema. Naturalmente, le distanze e possono essere calcolate anche in K', ma in questo caso bisogna tenere presente che si riferiscono ad eventi non simultanei e pertanto il calcolo risulta più complesso. In definitiva si dimostra che nel sistema K' dello sciatore, qualora si tenga conto della non simultaneità della misura degli estremi dello sci dovuta al tempo di propagazione finito della luce, questo cade nella buca solo se risulta .

La settimana prossima ci occuperemo del paradosso dei gemelli, con il quale concluderemo questo breve excursus nello strano mondo della relatività ristretta.

Leggi la prossima puntata...