Sarà perché è estate e i (tele)giornali non hanno molto di cui parlare ad esclusione, ovviamente, dell'importantissime vacanze dei VIP. Sarà perché gli oltre 120 milioni di montepremi fanno gola un po' a tutti. Sarà perché, in fondo, provare costa tanto poco o sarà un po' quello che volete, ma nessuno sembra essere estraneo alla mania del superenalotto estivo! Se ho letto bene le cifre, per l'estrazione di ieri sera (sabato 8 agosto) sono state giocate oltre 120 milioni di combinazioni, equivalente a dire che ogni italiano ha messo in gioco ben due sestine nella speranza di portare a casa il malloppo.
Ma conviene davvero giocare al superenalotto? Quanti sono le reali possibilità di vincere? Per rispondere in termini scientifici e rigorosi a queste domande serve che facciamo un po' di chiarezza e introduciamo qualche termine tecnico per poter descrivere matematicamente il problema. Innanzitutto diciamo che la probabilità di vincere è uguale al numero di combinazioni vincenti diviso il numero totale di combinazione possibili. Ovvero, prendiamo il caso di un gioco semplice come il lancio di un dado: se scommetto che uscirà il numero x (con x compreso tra 1 e 6 estremi inclusi
) allora avrò una probabilità di vincere uguale a 1 diviso 6, perché 6 sono tutti i possibili risultati. Se scommetto che uscirà un numero pari allora avrò tre possibili risultati vincenti (2, 4 e 6) su un totale di 6 possibili risultati, ovvero una probabilità del 50%.
Passare al superenalotto complica un po' le cose, ma cerchiamo di tenerle il più semplici possibili. Innanzitutto il numero delle uscite vincenti è precisamente 1, se puntiamo al fatidico 6. Esiste una e una sola sestina vincente per ogni estrazione.
Ma quante sono tutte le possibili combinazioni? Ovvero, ci stiamo chiedendo in quanti modi posso prendere 6 numeri da un totale di 90. Nel
calcolo combinatorio, questa operazione prende il nome di Combinazione semplice senza ripetizione e si calcola nel modo seguente:
dove n nel caso del superenalotto è uguale a 90, ovvero il numero totale di numeri, e k è 6 perché viene sempre estratta una sestina. Il simbolo ! nella seconda parte dell'equazione qui sopra identifica l'operazione
fattoriale, cioè, per esempio, il fattoriale di 10 è il prodotto degli interi positivi da 10 a 1, che come potete immaginare è un numero parecchio grande. Nel nostro caso specifico le possibili combinazioni di 6 elementi da un gruppo di 90 sono precisamente:
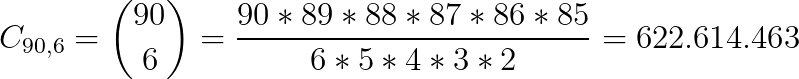
Si avete letto bene, 622 milioni e rotti! Quindi la probabilità di fare sei è di una su 622 milioni e se volessi esprimerla con un numero decimale dovrei scrivere zero virgola, otto zeri prima di poter, finalmente mettere un bel 1.
Se per l'ultima estrazione sono state giocate 120 milioni di combinazioni, assumendo per assurdo che queste fossero tutte diverse, allora la probabilità che ci fosse un fortunato vincitore si aggirava intorno al 20%.
Una curiosità: il meccanismo di estrazione non conosce quali numeri sono stati estratti e dal punto di vista probabilistico non esistono sestine strane o particolari. Questo per dire che si ha esattamente la stessa - ridicola - probabilità di vincere puntando su una senstina apparentemente normale o su una assolutamente bizzarra composta dai numeri 1, 2, 3, 4, 5 e 6! Vi può anche sembrare strano, ma il fatto che il primo numero estratto sia un 1, non cambia minimamente la probabilità che il secondo sia un 2 e così via. Tenete conto che nel superenalotto non conta l'ordine di estrazione per la sestina.
Andiamo, però avanti con le probabilità, perché non si vince solo con il 6.
Quant'è la probabilità di fare 5? Innazitutto partiamo dal fatto che sempre e comunque viene estratta una sestina e che quindi il numero delle possibili combinazioni resta immutato e uguale a 622 milioni e spiccioli. Quello che cambia in questo caso è che ci sono molte più combinazioni vincenti. Facciamo un esempio pratico: abbiamo giocato la nostra sestina fortunata 1, 2, 3, 4, 5 e 6. Allora vinceremo con il 5 se almeno cinque dei nostri numeri sono contenuti nella sestina vincente, questo vuol dire che se la sestina vincente è 1, 2, 3, 4, 5 e 85 andremo a ritirare il premio e lo faremo anche se al posto dell'85 ci fosse il 7 o il 24, insomma qualunque altro numero compreso tra 7 e 90, estremi inclusi. Avremo cioè 84 possibilità di vincere azzeccando i primi 5 numeri della sestina, ma la stessa cosa succede anche se indoviniamo i primi 4 e l'ultimo, come per esempio con la sestina 1, 2, 3, 4, 12 e 6. Ripetendo il ragionamento spostando il numero, ahime sbagliato, in tutte le posizioni, scopriamo che esistono 6 * 84 = 504 possibili sestine che ci permettono di incassare il premio per il 5. Allora in base alla nostra definizione di probabilità di vittoria, possiamo concludere che la probabilità di fare un bel 5 è
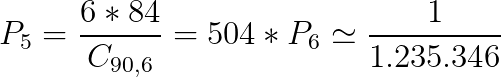
ovvero 504 volte superiore a quella di fare 6 e circa una su 1 milione e duecentomila!
 E il 5+1?
E il 5+1? Qui le cose si fanno decisamente più complicate, ma allo stesso tempo divertenti. Il premio del cinque più uno viene assegnato allo scommettitore che abbia indovinato 5 dei 6 numeri della sestina vincente e il numero jolly. Questo numero jolly è un settimo estratto, quindi differente da tutti gli altri già presenti nella sestina.
Dobbiamo quindi parlare di settimine, ovvero di raggrupamenti di sette numeri? Più o meno sì. Il fatto è che quando abbiamo fatto il ragionamento per il "5", non ci interessava per nulla quale dei cinque numero su sei avevamo indovinato, adesso invece per fare il "5+1" dobbiamo necessariamente indovinare l'ultimo numero estratto, il jolly, altrimenti al più potremo fare un "5", ma non un "5+1". Si tratta, matematicamente parlando, quindi di una settimina solo parzialmente ordinata, ovvero non ci interessa quale dei cinque numeri dei nostri primi sei sono veramente stati estratti, ma ci serve aver indovinato il settimo estratto! Questo trucchetto cambia innanzitutto il numero delle possibili estrazioni che saranno i soli 622 milioni per i primi 6 estratti senza ordine moltiplicati per gli 84 valori possibili del numero jolly. Ma quante di queste sono utili per il mio 5+1? In altre parole quante sono le settimine a me favorevoli in vista del “5+1”, quando scelgo 6 numeri e li gioco? Immaginiamo di scegliere i miei soliti numeri 1, 2, 3, 4, 5 e 6, allora una sestina + jolly vincente al 5+1 sarà per esempio la: 1, 2, 3, 4, 5 e 76 numero jolly = 6, ma vincerò anche se esce 29,2,3,4,5,6 numero jolly = 1. In definitiva vincerò quando verrà estratta una settimina contenente 6 termini iniziali (quelli di cui non importa l'ordine) costituiti da 5 tra i 6 numeri da me scelti, insieme con un numero che sta fra gli 84 numeri da me non scelti e da un numero finale coincidente col numero rimanente della mia sestina. Queste sono relativemante poche e per la precisione 6 * 84. Riassumendo:
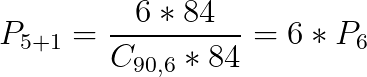
La prossima domanda che viene spontanea è:
ma conviene giocare? Visto che le possibilità di sbancare la cassa sono così irrisorie la risposta è che sarebbe da stupidi farne una professione. Mi spiego: giocare sistemi complessi pagando la scommessa diverse centinaia se non migliaia di euro è una vera e propria stupidaggine. Sono solo soldi buttati nel ... ecco avete capito cosa indentevo dire. Se invece vi accontenta di tentare la fortuna con un euro nell'assoluta certezza di perdere, allora può forse valere la pena sperare nella dea bendata.
Ma il superenalotto è un gioco onesto? Assolutamente no! Però prima di spiegarvi il motivo ho bisogno di definirvi cosa sia un gioco, probabilisticamente parlando, onesto. Nella teoria dei giochi diremo che un gioco è onesto se paga il vincitore in modo proporzionale alla probabilità di vincere. Se, per farla facile torniamo all'esempio iniziale del lancio del dado, in un gioco onesto indovinare un numero dovrebbe essere pagato 6 volte la posta e indovinare un pari o un dispari solo 2 volte. I giochi d'azzardo non possono, per definizione essere onesti, perché in un gioco onesto, lo scommettitore e il banco hanno esattamente lo stesso tornaconto, ovvero nessuno, in media, vince. Questo non può funzionare perché il casino ha bisogno di pagare gli stipendi, oltre che arricchire il suo proprietario e lo stato vuole anche la sua bella fetta di guadagno. Per questo motivo le case di scommesse devono spostare un po' la fortuna dalla loro parte, rendendo disonesti tutti i giochi d'azzardo, ovvero pagando le vincite in modo non proporzionale alla probabilità di ottenerle. Sarebbe come a dire che indovinare un numero sul lancio dei dadi viene pagato solo 5.5 volte la posta e non esattamente 6 come onestà vorrebbe. Stimare l'equità del superenalotto è un po' più complesso perché la vincita è basata su un montepremi che si accumula anziché essere proporzionale alla difficoltà della scommessa.
Ma i numeri che sto per darvi possono darvi un'indicazione dell'iniquità del gioco. Ogni 100 euro giocati ben 53 euro e 60 centesimi finiscono direttamente nelle casse dello Stato, 8 euro restano nelle tasche della ricevitoria che ha accettato la scommessa, 3 euro e 73 centesimi vanno alla Sisal e solo i restanti 34 euro e 65 finiscono nel calderone delle vincite. Per dirla in altre parole solo un terzo dei soldi che giochiamo possono ritornare nelle nostre tasche sotto forma di vincita.
 Ma come funziona il montepremi?
Ma come funziona il montepremi? Giuro che questa però è l'ultima domanda a cui vi rispondo. Per capirlo serve leggere nel dettaglio gli articoli 3 e 4 del
regolamento ufficiale del superenalotto. Prendiamo per semplicità di conti una estrazione per cui sono state giocate 100 milioni di combinazioni (20 milioni in meno di quelle giocate sabato scorso); visto che ciascuna giocata costa 50 eurocent, vengono scommessi in totale 50 milioni di euro. Di questi, come già detto nella domanda precedente solo il 34,648% viene rimesso in palio sottoforma di montepremi, ovvero 17 milioni e 324 mila euro. Questi soldi vengono ulteriormente divisi tra le varie categorie di premi, secondo la tabella seguente:
- Prima categoria "6": 20%, ovvero 3.464.800 euro
- Seconda categoria "5+1": 20% ovvero 3.464.800 euro
- Terza categoria "5": 15% ovvero 2.598.600 euro
- Quarta categoria "4": 15% ovvero 2.598.600 euro
- Quinta categoria "3": 30% ovvero 5.197.200 euro
Ovviamente, in caso ci siano due vincitori della stessa categoria, questi si divideranno in parti uguali il montepremi della loro categoria. C'è poi il meccanismo dell'accumulo, ovvero se in una estrazione non ci sono vincitori di prima categoria (nessun sei, per intenderci) allora il montepremi di questa giocata andrà a sommarsi con quello della prossima dando vita così al jackpot milionario. Questo meccanismo si ripete fino a quando, finalmente, ci sarà un fortunato vincitore con 6 numeri estratti, e visto quanto improbabile questo fenomeno sia, è abbastanza naturale aspettarsi jackpot multimilionari.
Una cosa abbastanza simile avviene anche per il "5+1", infatti se nessun giocatore realizza questa vincita allora il montepremi di seconda categoria viene diviso in due parti uguali: una che andrà a sommarsi con il montepremi del prossimo concorso e una, invece, andrà a costituire un fondo finalizzato all'incremento del montepremi di prima categoria del concorso successivo all'avvenuta assegnazione di un 6. Questo è il motivo per cui, quando il 6 manca per parecchio tempo, anche dopo che viene assegnato, il jackpot resta comunque molto interessante dal punto di vista economico.
Per le categorie minori, la cosa si complica ulteriormente, ma le cifre in gioco sono generalmente sufficientemente piccole da rendere questo meccanismo complicato poco interessante.
Un'ultima curiosità:
le vincite non sono tasste e sono pagate in contanti e non in gettoni d'oro. E il superstar? Basta vi avevo dette che quella di prima era l'ultima domanda... se portate pazienza un giorno ve lo spiego...
 Il quattro è proprio un bel numero e ci sono tanti motivi per giustificare questa sua bellezza. Per esempio, è il più piccolo numero intero non primo (escludendo l'1, che è un caso molto particolare); è il piccolo quadrato perfetto pari (se non ci fossero 0 e 1 sarebbe anche il più piccolo in generale); insieme a 3 e a 5 appartiene alla prima terna pitagorica. E questo solo nel mondo matematico. In biologia, quattro è il numero delle basi che compongono il DNA e anche il numero delle stanze in cui è diviso il cuore dei mammiferi. Nel mondo dei fumetti, il numero quattro è indissolubilmente legato ai Fantastici supereroi della Marvel.
Il quattro è proprio un bel numero e ci sono tanti motivi per giustificare questa sua bellezza. Per esempio, è il più piccolo numero intero non primo (escludendo l'1, che è un caso molto particolare); è il piccolo quadrato perfetto pari (se non ci fossero 0 e 1 sarebbe anche il più piccolo in generale); insieme a 3 e a 5 appartiene alla prima terna pitagorica. E questo solo nel mondo matematico. In biologia, quattro è il numero delle basi che compongono il DNA e anche il numero delle stanze in cui è diviso il cuore dei mammiferi. Nel mondo dei fumetti, il numero quattro è indissolubilmente legato ai Fantastici supereroi della Marvel.